データサイエンス×教育：取り組みから実感した教育分野のPoCのおもしろさ

こんにちは。データサイエンティストの石井です。今回は、複数の問題を組合せた問題の集合（以降、問題集という）を推薦するアイデアのPoCに取り組みました。今回の取り組みの中ではこのアイデアが有効かの判断には至りませんでしたが、具体的にどのような取り組みを行ったのか、またそこで直面した教育分野のPoC特有のおもしろさについて紹介します。

なぜ問題集の推薦に取り組むのか

2023年5月31日に公開したプレスリリースのとおり、新しい学び支援機能としてAI搭載の「学習トレーニング」機能の提供を始めました。

参考：生徒の自律性とAIによる個別最適な学びを両立する「学習トレーニング」機能を6月にリリース

この機能に搭載されているAIは、生徒一人一人に合わせた問題を1問ずつ推薦するものです。また、このAIは問題に取り組むごとにそれまでの解答データから「その生徒にある問題を出題した時に何%の確率で正解できそうか」を計算し、その予測正答確率の値にもとづき、難しすぎず易しすぎない問題を推薦します。このAIを搭載した「学習トレーニング」機能では、特に取り組む問題数の上限を設けず、何問でも推薦された問題に取り組むことができます。一方、私の学生時代を振り返ると、ページ数や学習時間をあらかじめ決めて学習に取り組んでいた記憶があります。そこで、もしあらかじめ問題数が決まっているのであれば、その問題数の問題を選定し、学習に取り組む方がより効果の高い学習ができるのではないか、と考えました。このような考えから、「生徒の実力に合わせて問題選定された問題集の推薦は、既存の1問ずつの推薦より、高い学習効果が得られるか」という仮説を立てました。

問題集編成のアプローチ

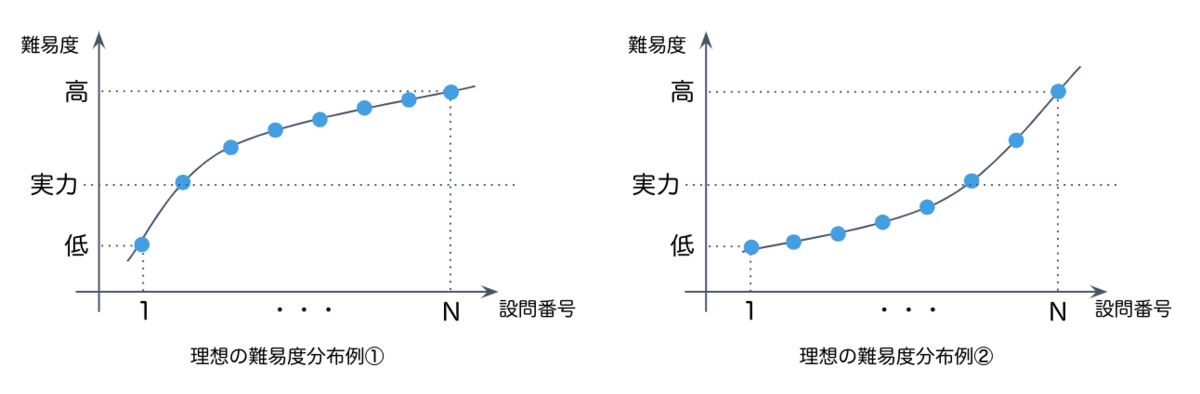
数理最適化技術を用いたモデルで、Classiに搭載されている大量の問題からいくつかの問題を選択し、問題集を編成していきます。編成したい問題集の設問数に応じて、どの難易度の問題をどの順序で出題するかを考慮します。例えば、ある生徒には対象生徒の実力より難しい問題を多く出題する場合（下図の例①）、また、ほかのある生徒には対象生徒の実力より易しい問題を多く出題する場合（下図の例②）など、設問と難易度の関係（以降、理想の難易度分布という）については、さまざまなケースが考えられます。この理想の難易度分布と選ぶ問題の難易度の差を最小化する整数計画問題を解くことで問題集を編成します。

モデルの詳細

定式化

与えられた問題集合を $I$ とし、編成する問題集の設問番号の集合を $J$ とします。変数 $x_{ij}$ を問題 $i$ を問題集の設問 $j$ に採用するなら1、非採用なら0となる2値変数とします $( i \in I, j \in J, |I| \ge |J|)$ 。理想の難易度分布 $f(j) (j \in J)$ 、問題 $i$ の難易度 $d_{i}$ を用いて、制約： $|f(j) - d_{i}|x_{ij} \leq \delta ( \forall i \in I , \forall j \in J)$ を満たす $\delta$ の最小化を目的関数とします。また、そのほかの制約には以下があります。

ある設問に1つの問題を割り当てる制約：

$\displaystyle \sum_{i \in I} x_{ij} = 1 ( \forall j \in J )$

ある問題はたかだか1つの設問にしか割り当てられない制約：

$\displaystyle \sum_{j \in J} x_{ij} \le 1 ( \forall i \in I )$

以上のことを整理すると、解くべき整数計画問題は次のようになります。

$\displaystyle \begin{eqnarray} & \text{Minimize} & \delta \nonumber \\ & \text{s.t.} & |f(j) - d_{i}|x_{ij} \leq \delta \left( \forall i \in I , \forall j \in J \right) \nonumber \\ && \sum_{i \in I} x_{ij} = 1 \left( \forall j \in J \right) \nonumber \\ && \sum_{j \in J} x_{ij} \le 1 \left( \forall i \in I \right) \nonumber \\ && x_{ij} \in \left\{ 0, 1 \right\} \left( \forall i \in I, \forall j \in J \right). \nonumber \end{eqnarray}$

マッチングのアルゴリズムにもとづく高速な解法

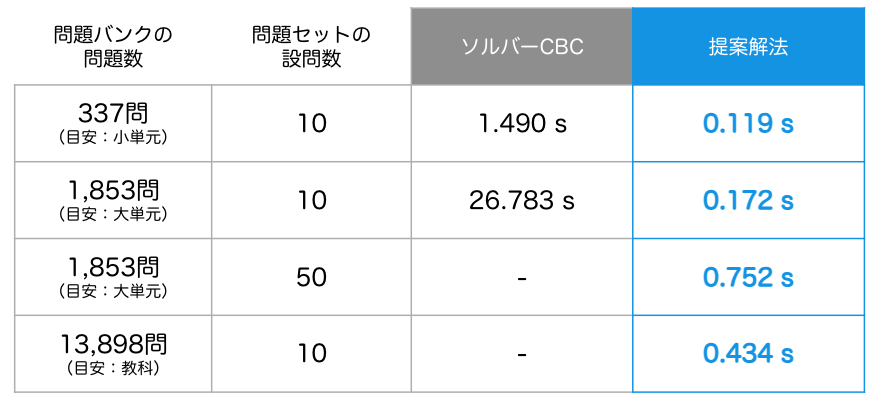
快適なサービス提供のために、ある単元に含まれる問題数 $|I| = 1853$ , 代表的なテストの設問数 $|J| = 10$ の設定で、0.7秒以内に解を求めることを目標にしました。しかし、先の定式化を汎用ソルバーCBCで解くと約26秒を要し、さらに問題数や設問数が多い場合には解を求めることができませんでした。そのため、マッチングのアルゴリズムにもとづく高速な解法を検討しました。この解法では、全設問への割り当てが存在するような難易度のずれの許容値 $\delta$ について、その最小値を二分探索で求めることを考えます。与えられた $\delta$ に対し、全設問への割り当てが存在するか否かを判定するには、まず、与えられた $\delta$ で2部グラフを構成します。次に、最大マッチングを求め、そのサイズが設問数と一致していれば、全設問への割り当てが存在することになり、そうでなければ所望の割り当ては存在しないことになります。 $\delta$ が最小のときの全設問への割り当ては、上で求めた最大マッチングの結果から求めることができます。

この解法を用いて、設問数を10問で固定し問題数を変動させるパターンと、問題数を1853問で固定し設問数を変動させるパターンの2つの実験を行いました。この解法では、下表のように、想定する問題数・設問数に対して0.7秒未満で求めることができ、さらに想定以上の問題数・設問数でも解を求めることができました。

PoCの実施

今回のPoCで、本来明らかにしたいことは「生徒の実力に合わせて問題選定された問題集の推薦は、既存の1問ずつの推薦より、高い学習効果が得られるか」、さらに、学習効果が高い場合に「どのような生徒に、どのような理想の難易度分布で編成した問題集が学習効果を最大化するのか」です。

学習効果があるか判断するためには、ある程度の期間でこの問題集を用いて学習に取り組んでもらう必要があります。また、その期間中はほかの学習コンテンツを使用せず、この問題集のみで学習してもらう必要があります。日々、学校や塾などで所定のカリキュラムで学習する生徒に対して、この検証環境を作ることは現実的ではありません。

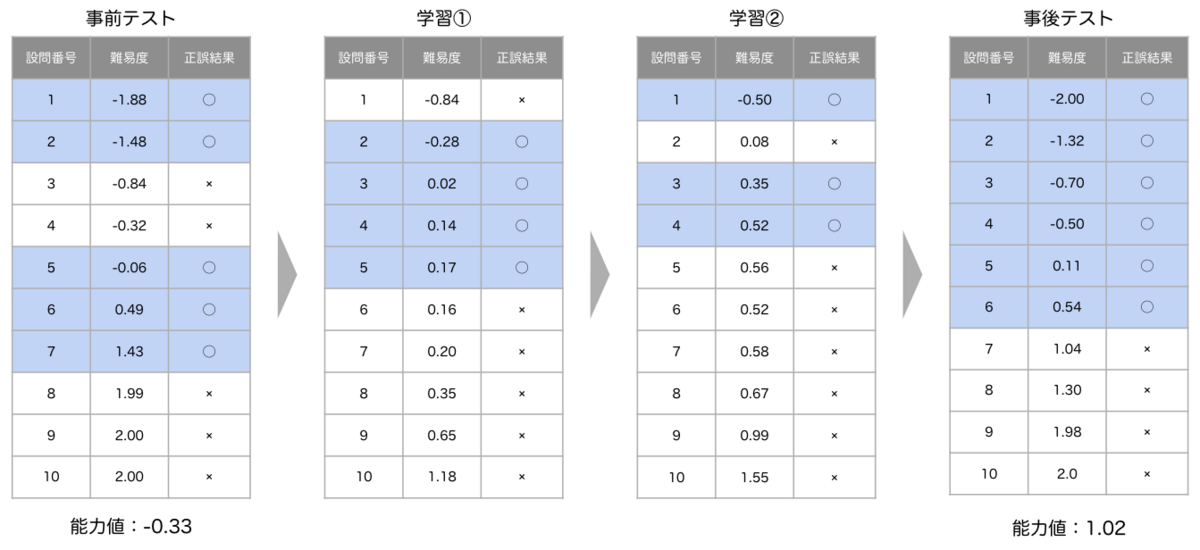
そこで今回は、数時間の検証でこの学習効果を測定できないか、検討しました。以下のタイムスケジュールで検証を行い、事前・事後テストの結果の差から学習効果を測ります。

事前テスト：30分(10問)
問題集での学習①：約45分(10問)
問題集での学習②：約45分(10問)
事後テスト：30分(10問)

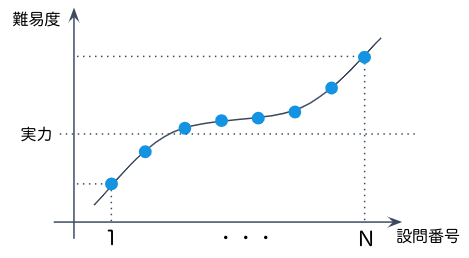
学習①では事前テストの結果から、学習②では学習①の結果から、問題集の難易度を決定します。また、理想の難易度分布は、下図のような、実力より易しい問題から始まり、中盤は実力より少し難しい問題を多く出題し、終盤に実力より難しい問題を出題する分布としました。

事前テストと事後テストで出題される問題は異なる等質なテスト（ある受験者に対し、同一の評価ができるテスト）を使用します。なお、この事前テスト・事後テストも整数計画問題として定式化し、編成しました。学習効果がある場合は、短期間で結果に出るように事前・事後テストと問題集の出題範囲を1つの単元に絞りました。今回は「数学A-場合の数」で実施しました。学習効果は、事前・事後テストの解答の正誤データをもとに、IRT（項目反応理論）にもとづき推定した能力値の増減で判定します。

検証の結果、1人目の能力値は 1.87→0.72と減少し、2人目の能力値は-0.33→1.02と増加しました。1人目の減少の理由はいくつか考えられます。

事前・事後テストの問題数が不足しており、正確に計測できなかった可能性
事前・事後テストが等質なテストではなく、正確に計測できなかった可能性
「数学A-場合の数」は全列挙で正答できてしまい、検証対象の単元として不適切であった可能性
学習時間が90分では足りず、実際に学習効果がなかった可能性

一方、2人目は正誤結果に違和感なく、能力値も増加しました。今回の事前検証から、短期間での検証で学習効果を計測できる可能性はあると感じています。しかし、教育におけるPoCの難しさを痛感し、短期間で学習効果を計測するPoCを行うには改善が必要だと思われます。

教育におけるPoCのおもしろさ

教育分野の学習コンテンツのPoCにおいて、その学習コンテンツの有効性を十分に判断するためには、学習効果を測る必要があります。しかし、上で述べたように学習効果を測ることは容易ではありません。学習効果を測る際には以下の観点のバランスをみて総合的に決定していく必要があります：

検証期間： 学習効果があるかを判断するために必要十分な学習期間を設定しなければなりません。期間が短すぎる場合は学習効果が十分に判断できず、反対に期間が長すぎる場合は後述の検証環境の構築が難しくなります。
出題範囲： 教科や単元（例：因数分解や場合の数など）の出題範囲が必要十分でなければなりません。出題範囲を広げた場合はそれだけ検証期間を要することとなり、出題範囲を狭めた場合は設定した単元に依存した検証結果となってしまいます。
被験者と検証環境： 純粋な学習効果を計測するためには、検証期間中、被験者を学校や塾などのほかの環境での学習から切り離さなければなりません。
学習効果の測定方法： 学習効果を測定する一般的な手法である「テスト」を使用するか、また、テストで行う場合には事前・事後テストが等質でなければなりません。

これらは、教育分野の学習に関するPoCにおいて重要な観点であり、決定するのは非常に難しいです。しかし、このような難しさが教育分野におけるデータサイエンスのおもしろさでもあります。教科や単元により、問題設定からモデルの構築までまったく異なる教育分野はデータサイエンスの宝庫です。

最後に

ClassiにおけるPoCの取り組みと、教育分野のPoC特有のおもしろさについて紹介しました。今回の数理最適化技術を応用したモデルの開発は、学校の先生や生徒との継続的な対話とモデルの改善を繰り返し行い、さらに、東京理科大学の池辺淑子准教授、西田優樹助教、法政大学の鮏川矩義准教授から数理最適化技術に関してアドバイスをいただき、共同で開発を進めました。このように、Classiでは生徒により良い学習体験を提供するために、学校の先生・生徒、そして学術機関と協力し、多くの取り組みを積極的に行っています。また、Classiではこのほかにも生成AIを用いたコンテンツ制作やClassiにおける学習データでの成績評価など、さまざまな取り組みを行っています。教育分野におけるプロダクト開発に興味をお持ちの方は、ぜひ採用ページをご覧ください。皆様からのご応募をお待ちしています。

https://hrmos.co/pages/classi/jobs